Tuples
Tuples in TLA+ are special kinds of functions that satisfy one of the following properties:
- The domain is either empty, that is,
{}, or - The domain is
1..nfor somen > 0.
That is right. You can construct the empty tuple <<>> in TLA+ as well as a
single-element tuple, e.g., <<1>>. You can also construct pairs, triples, an
so on, e.g., <<1, TRUE>>, <<"Hello", "world", 2020>>. If you think that
empty tuples do not make sense: In TLA+, there is no difference between tuples
and sequences. Again, it is duck typing: Any function with
the domain 1..n can be also treated as a tuple (or a sequence!), and vice
versa, tuples and sequences are also functions. So you can use all function
operators on tuples.
Importantly, the domain of a nonempty tuple is 1..n for some n > 0. So tuples never
have a 0th element. For instance, <<1, 2>>[1] gives us 1, whereas <<1, 2>>[2] gives us 2.
Construction. TLA+ provides you with a convenient syntax for constructing
tuples. For instance, the following example shows how to construct a tuple
that has two fields: Field 1 is assigned value 2, and field 2 is
assigned value TRUE.
<<2, TRUE>>
There is a tuple set constructor, which is well-known as Cartesian product:
{ "Alice", "Bob" } \X (1900..2000)
The expression in the above example constructs a set of tuples <<n, y>>: the
first field n is set to either "Alice" or "Bob", and the second field y is set
to an integer from 1900 to 2000.
Application. Simply use function application, e.g., t[2].
Immutability. As tuples are special kinds of functions, tuples are immutable.
Types. In contrast to pure TLA+ and TLC, the Apalache model checker
distinguishes between general functions, tuples, and sequences. They all have
different types. Essentially, a function has the type A -> B that
restricts the arguments and results as follows: the arguments have the type
A and the results have the type B. A sequence has the type
Seq(C), which restricts the sequence elements to have the same type C. In
contrast, tuples have more fine-grained types in Apalache: <<T_1>>, <<T_1, T_2>>, <<T_1, T_2, T_3>> and so on. As a result, different tuple fields are
allowed to carry elements of different types, whereas functions and sequences
are not allowed to do that. See the Apalache ADR002 on types for details.
As tuples are also sequences in TLA+, this poses a challenge for the Apalache
type checker. For instance, it can immediately figure out that <<1, "Foo">>
is a tuple, as Apalache does not allow sequences to carry elements of different
types. However, there is no way to say, whether <<1, 2, 3>> should be treated
as a tuple or a sequence. Usually, this problem is resolved by annotating the
type of a variable or the type of a user operator. See HOWTO write type
annotations.
Owing to the type information, tuples are translated into SMT much more efficiently by Apalache than the general functions and sequences!
Operators
In the Python examples, we are using the package frozendict, to produce an immutable dictionary.
Tuple/Sequence constructor
Notation: <<e_1, ..., e_n>>
LaTeX notation: 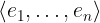
Arguments: An arbitrary number of arguments.
Apalache type: This operator is overloaded. There are two potential types:
- A tuple constructor:
(a_1, ..., a_n) => <<a_1, ..., a_n>>, for some typesa_1, ..., a_n. - A sequence constructor:
(a, ..., a) => Seq(a), for some typea.
That is why the Apalache type checker is sometimes asking you to add annotations, in order to resolve this ambiguity.
Effect: The tuple constructor returns a function t that is constructed
as follows:
- set
DOMAIN tto1..n, - set
r[i]to the value ofe_ifori \in 1..n.
In Apalache, this constructor may be used to construct either a tuple, or a sequence. To distinguish between them, you will sometimes need a [type annotation].
Determinism: Deterministic.
Errors: No errors.
Example in TLA+:
<<"Printer", 631>>
Example in Python: Python provides us with the syntax for constructing tuples, which are indexed with 0!. If we want to stick to the principle "tuples are functions", we have to use a dictionary.
>>> ("Printer", 631) # the pythonic way, introducing fields 0 and 1
('Printer', 631)
>>> { 1: "Printer", 2: 631 } # the "tuples-are-functions" way
{1: 'Printer', 2: 631}
Cartesian product
Notation: S_1 \X ... \X S_n (or S_1 \times ... \times S_n)
LaTeX notation: 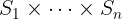
Arguments: At least two arguments. All of them should be sets.
Apalache type: (Set(a_1), ..., Set(a_n)) => Set(<<a_1, ..., a_n>>),
for some types a_1, ..., a_n.
Effect: The Cartesian product S_1 \X ... \X S_n
is syntax sugar for the set comprehension:
{ << e_1, ..., e_n >> : e_1 \in S_1, ..., e_n \in S_n }
Determinism: Deterministic.
Errors: The arguments S_1, ..., S_n must be sets. If they are not sets,
the result is undefined in pure TLA+. TLC raises a model checking error. Apalache
flags a static type error.
TLC raises a model checking error, whenever one of the sets S_1, ..., S_n is
infinite. Apalache can handle infinite sets in some cases, e.g., when one tuple
is picked with \E t \in S_1 \X S_2.
Example in TLA+:
{ "A", "B", "C" } \X (1..65535)
\* A set of tuples. Each tuple has two fields:
\* - field 1 has the value from the set { "A", "B", "C" }, and
\* - field 2 has the value from the set 1..65535.
Example in Python: TLA+ functions are immutable, so we are using frozendict:
# the pythonic way: a set of python tuples (indexed with 0, 1, ...)
frozenset({ (n, p)
for n in { "A", "B", "C" } for p in range(1, 65535 + 1) })
# the TLA+ way
frozenset({ frozendict({ 1: n, 2: p })
for n in { "A", "B", "C" } for p in range(1, 65535 + 1) })
Function application
As tuples are functions, you can access tuple elements by function
application, e.g., tup[2]. However, in the case of a
tuple, the type of the function application will be: (<<a_1, ..., a_i, ..., a_n>>, Int) => a_i, for some types a_1, ..., a_n.