Integers
The integer literals belong to the core language. They are written by
using the standard syntax: 0, 1, -1, 2, -2, 3, -3, ... Importantly, TLA+
integers are unbounded. They do not have any fixed bit width, and they cannot
overflow. In Apalache, these literals have the type Int.
The integer operators are defined in the standard module Integers. To use
it, write the EXTENDS clause in the first lines of your module. Like this:
---- MODULE MyArithmetics ----
EXTENDS Integers
...
==============================
Integers in Apalache and SMT
Although you can write arbitrary expressions over integers in TLA+, Apalache
translates these expressions as constraints in
SMT.
Some expressions are easier to solve than others.
For instance, the expression 2 * x > 5 belongs to linear integer arithmetic,
which can be solved more efficiently than general arithmetic.
For state variables x and y, the expression x * y > 5 belongs to
non-linear integer arithmetic, which is harder to solve than linear arithmetic.
When your specification is using only integer literals, e.g., 1, 2, 42,
but none of the operators from the Integers module, the integers can
be avoided altogether. For instance, you can replace the integer constants
with string constants, e.g., "1", "2", "42". The string constants are
translated as constants in the SMT constraints. This simple trick may bring
your specification into a much simpler theory. Sometimes, this trick allows z3
to use parallel algorithms.
Constants
The module Integers defines two constant sets (technically, they are
operators without arguments):
- The set
Intthat consists of all integers. This set is infinite. In Apalache, the setInthas the typeSet(Int). A bit confusing, right? 😎 - The set
Natthat consists of all natural numbers, that is,Natcontains every integerxthat has the propertyx >= 0. This set is infinite. In Apalache, the setNathas the type...Set(Int).
Operators
Integer range
Notation: a..b
LaTeX notation: a..b
Arguments: Two arguments. The result is only defined when both arguments are evaluated to integer values.
Apalache type: (Int, Int) => Set(Int).
Effect: a..b evaluates to the finite set {i \in Int: a <= i /\ i <= b},
that is, the set of all integers in the range from a to b, including a
and b. If a > b, then a..b is the empty set {}.
Determinism: Deterministic.
Errors: In pure TLA+, the result is undefined if one of the arguments evaluates to a non-integer value. In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
0..10 \* { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }
-5..3 \* { -5, -4, -3, -2, -1, 0, 1, 2, 3 }
10..0 \* { }
"a".."z" \* runtime error in TLC, type error in Apalache
{1}..{3} \* runtime error in TLC, type error in Apalache
Example in Python: a..b can be written as set(range(a, b + 1)) in
python.
>>> set(range(0, 10 + 1))
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
>>> set(range(10, 2))
set()
Unary integer negation
Notation: -i
LaTeX notation: -i
Arguments: One argument. The result is only defined when the argument evaluates to an integer.
Apalache type: Int => Int.
Effect: -i evaluates to the negation of i.
Determinism: Deterministic.
Errors: In pure TLA+, the result is undefined if the argument evaluates to a non-integer value. In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
-(5) \* -5, note that '-5' is just a literal, not operator application
-(-5) \* 5
-x \* negated value of x
Example in Python:
>>> -(5)
-5
>>> -(-5)
5
Integer addition
Notation: a + b
LaTeX notation: a + b
Arguments: Two arguments. The result is only defined when both arguments are evaluated to integer values.
Apalache type: (Int, Int) => Int.
Effect: a + b evaluates to the sum of a and b.
Determinism: Deterministic.
Errors: No overflow is possible. In pure TLA+, the result is undefined if one of the arguments evaluates to a non-integer value. In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
5 + 3 \* 8
(-5) + 3 \* -2
Example in Python:
>>> 5 + 3
8
>>> (-5) + 3
-2
Integer subtraction
Notation: a - b
LaTeX notation: a - b
Arguments: Two arguments. The result is only defined when both arguments are evaluated to integer values.
Apalache type: (Int, Int) => Int.
Effect: a - b evaluates to the difference of a and b.
Determinism: Deterministic.
Errors: No overflow is possible. In pure TLA+, the result is undefined if one of the arguments evaluates to a non-integer value. In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
5 - 3 \* 2
(-5) - 3 \* -8
(-5) - (-3) \* -2
Example in Python:
>>> 5 - 3
2
>>> (-5) - 3
-8
>>> (-5) - (-3)
-2
Integer multiplication
Notation: a * b
LaTeX notation: a * b
Arguments: Two arguments. The result is only defined when both arguments are evaluated to integer values.
Apalache type: (Int, Int) => Int.
Effect: a * b evaluates to the product of a and b.
Determinism: Deterministic.
Errors: No overflow is possible. In pure TLA+, the result is undefined if one of the arguments evaluates to a non-integer value. In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
5 * 3 \* 15
(-5) * 3 \* -15
Example in Python:
>>> 5 * 3
15
>>> (-5) * 3
-15
Integer division
Notation: a \div b
LaTeX notation: 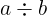
Arguments: Two arguments. The result is only defined when both arguments are evaluated to integer values, and the second argument is different from 0.
Apalache type: (Int, Int) => Int.
Effect: a \div b is defined as follows:
- When
a >= 0andb > 0, then the result ofa \div bis the integercthat has the property:a = b * c + dfor somedin0..(b-1). - When
a < 0andb > 0, then the result ofa \div bis the integercthat has the property:a = b * c + dfor somedin0..(b-1). - When
a >= 0andb < 0, then the result ofa \div bis the integercthat has the property:a = b * c + dfor somedin0..(-b-1). - When
a < 0andb < 0, then the result ofa \div bis the integercthat has the property:a = b * c + dfor somedin0..(-b-1).
When a < 0 or b < 0, the result of the integer division a \div b according to the TLA+ definition is different from the integer division a / b in the programming languages (C, Java, Scala, Rust). See the
table below.
| C (clang 12) | Scala 2.13 | Rust | Python 3.8.6 | TLA+ (TLC) | SMT (z3 4.8.8) |
|---|---|---|---|---|---|
| 100 / 3 == 33 | 100 / 3 == 33 | 100 / 3 == 33 | 100 // 3 == 33 | (100 \div 3) = 33 | (assert (= 33 (div 100 3))) |
| -100 / 3 == -33 | -100 / 3 == -33 | -100 / 3 == -33 | -100 // 3 == -34 | ((-100) \div 3) = -34 | (assert (= (- 0 34) (div (- 0 100) 3))) |
| 100 / (-3) == -33 | 100 / (-3) == -33 | 100 / (-3) == -33 | 100 // (-3) == -34 | (100 \div (-3)) = -34 | (assert (= (- 0 33) (div 100 (- 0 3)))) |
| -100 / (-3) == 33 | -100 / (-3) == 33 | -100 / (-3) == 33 | -100 // (-3) == 33 | ((-100) \div (-3)) = 33 | (assert (= 34 (div (- 0 100) (- 0 3)))) |
Unfortunately, Specifying Systems only gives us the definition for the case
b > 0 (that is, cases 1–2 in our description).
The implementation in SMT and TLC produce incompatible results for b < 0.
See issue #331 in Apalache.
Determinism: Deterministic.
Errors: No overflow is possible. In pure TLA+, the result is undefined if
one of the arguments evaluates to a non-integer value. In this case, Apalache
statically reports a type error, whereas TLC reports a runtime error. The value
of a \div b is undefined for b = 0.
Example in TLA+: Here are the examples for the four combinations of signs (according to TLC):
100 \div 3 \* 33
(-100) \div 3 \* -34
100 \div (-3) \* -34 in TLC
(-100) \div (-3) \* 33 in TLC
Example in Python: Here are the examples for the four combinations of signs to produce the same results as in TLA+:
>>> 100 // 3
33
>>> -100 // 3
-34
>>> 100 // (-3)
-34
>>> (-100) // (-3)
33
Integer remainder
Notation: a % b
LaTeX notation: a % b
Arguments: Two arguments. The result is only defined when both arguments are evaluated to integer values, and the second argument is different from 0.
Apalache type: (Int, Int) => Int.
Effect: a % b is the number c that has the property:
a = b * (a \div b) + c.
Note that when a < 0 or b < 0, the result of the integer remainder a % b
according to the TLA+ definition is different from the integer remainder a % b in the programming languages (C, Python, Java, Scala, Rust). See the
examples below.
Determinism: Deterministic.
Errors: No overflow is possible. In pure TLA+, the result is undefined if
one of the arguments evaluates to a non-integer value. In this case, Apalache
statically reports a type error, whereas TLC reports a runtime error. The value
of a % b is undefined for b = 0.
Example in TLA+: Here are the examples for the four combinations of signs:
100 % 3 \* 1
-100 % (-3) \* 2
100 % (-3) \* 1
-100 % 3 \* 2
Example in Python: Here are the examples for the four combinations of signs to produce the same results as in TLA+:
>>> 100 % 3
1
>>> -100 % (-3) + 3
2
>>> 100 % (-3) + 3
1
>>> -100 % 3
2
Integer exponentiation
Notation: a^b
LaTeX notation: 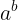
Arguments: Two arguments. The result is only defined when both arguments are evaluated to integer values, and these values fall into one of the several cases:
b > 0,b = 0anda /= 0.
Apalache type: (Int, Int) => Int.
Effect: a^b evaluates to a raised to the b-th power:
- If
b = 1, thena^bis defined asa. - If
a = 0andb > 0, thena^bis defined as0. - If
a /= 0andb > 1, thena^bis defined asa * a^(b-1). - In all other cases,
a^bis undefined.
In TLA+, a^b extends to reals, see Chapter 18 in Specifying Systems.
For instance, 3^(-5) is defined on reals. However, reals are supported
neither by TLC, nor by Apalache.
Determinism: Deterministic.
Errors: No overflow is possible. In pure TLA+, the result is undefined if one of the arguments evaluates to a non-integer value. In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
5^3 \* 125
(-5)^3 \* -125
0^3 \* 0
1^5 \* 1
(-1)^5 \* -1
0^0 \* undefined on integers, TLC reports a runtime error
5^(-3) \* undefined on integers, TLC reports a runtime error
Example in Python:
>>> 5 ** 3
125
>>> (-5) ** 3
-125
>>> 0 ** 3
0
>>> 1 ** 5
1
>>> (-1) ** 5
-1
>>> 0 ** 0
1
>>> 5 ** (-3)
0.008
Integer less-than
Notation: a < b
LaTeX notation: a < b
Arguments: Two arguments. The result is only defined when both arguments are evaluated to integer values.
Apalache type: (Int, Int) => Bool.
Effect: a < b evaluates to:
TRUE, ifais less thanb,FALSE, otherwise.
Determinism: Deterministic.
Errors: In pure TLA+, the result is undefined if one of the arguments evaluates to a non-integer value. In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
1 < 5 \* TRUE
5 < 5 \* FALSE
5 < 1 \* FALSE
Example in Python:
>>> 1 < 5
True
>>> 5 < 5
False
>>> 5 < 1
False
Integer less-than-or-equal
Notation: a <= b or a =< b or a \leq b
LaTeX notation: 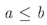
Arguments: Two arguments. The result is only defined when both arguments are evaluated to integer values.
Apalache type: (Int, Int) => Bool.
Effect: a <= b evaluates to:
TRUE, ifa < bora = b.FALSE, otherwise.
Determinism: Deterministic.
Errors: No overflow is possible. In pure TLA+, the result is undefined if one of the arguments evaluates to a non-integer value. In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
1 <= 5 \* TRUE
5 <= 5 \* TRUE
5 <= 1 \* FALSE
Example in Python:
>>> 1 <= 5
True
>>> 5 <= 5
True
>>> 5 <= 1
False
Integer greater-than
Notation: a > b
LaTeX notation: a > b
Arguments: Two arguments. The result is only defined when both arguments are evaluated to integer values.
Apalache type: (Int, Int) => Bool.
Effect: a > b evaluates to:
TRUE, ifais greater thanb,FALSE, otherwise.
Determinism: Deterministic.
Errors: No overflow is possible. In pure TLA+, the result is undefined if one of the arguments evaluates to a non-integer value. In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
1 > 5 \* FALSE
5 < 5 \* FALSE
5 > 1 \* TRUE
Example in Python:
>>> 1 > 5
False
>>> 5 > 5
False
>>> 5 > 1
True
Integer greater-than-or-equal
Notation: a >= b or a \geq b
LaTeX notation: 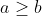
Arguments: Two arguments. The result is only defined when both arguments are evaluated to integer values.
Apalache type: (Int, Int) => Bool.
Effect: a >= b evaluates to:
TRUE, ifa > bora = b.FALSE, otherwise.
Determinism: Deterministic.
Errors: No overflow is possible. In pure TLA+, the result is undefined if one of the arguments evaluates to a non-integer value. In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
1 >= 5 \* FALSE
5 >= 5 \* TRUE
5 >= 1 \* TRUE
Example in Python:
>>> 1 >= 5
False
>>> 5 >= 5
True
>>> 5 >= 1
True
Equality and inequality
The operators a = b and a /= b are core operators of TLA+, and thus they are
not defined in the module Integers, see Logic.