Booleans
You find these operators in every programming language and every textbook on logic. These operators form propositional logic.
Constants
TLA+ contains three special constants: TRUE, FALSE, and BOOLEAN.
The constant BOOLEAN is defined as the set {FALSE, TRUE}.
In Apalache, TRUE, FALSE, and BOOLEAN have the types Bool, Bool,
and Set(Bool), respectively.
A note for set-theory purists: In theory, TRUE and FALSE are also sets, but
in practice they are treated as indivisible values. For instance, Apalache and
TLC will report an error, if you try to treat FALSE and TRUE as sets.
Operators
Warning: Below, we discuss Boolean operators in terms of the way they are usually
defined in programming languages. However, it is important to understand that the
disjunction operator F \/ G induces a nondeterministic effect when F or G contain
the prime operator ('), or when they are used inside the initialization predicate Init.
We discuss this effect Control Flow and Non-determinism.
And (conjunction)
Notation: F /\ G or F \land G
LaTeX notation: 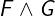
Arguments: Two or more arbitrary expressions.
Apalache type: (Bool, Bool) => Bool
Effect: The binary case F /\ G evaluates to:
-
TRUE, if bothFandGevaluate toTRUE. -
FALSE, ifFevaluates toFALSE, orFevaluates toTRUEandGevaluates toFALSE.
The general case F_1 /\ ... /\ F_n can be understood by evaluating
the expression F_1 /\ (F_2 /\ ... /\ (F_{n-1} /\ F_n)...).
Determinism: Deterministic, if the arguments are deterministic. Otherwise, the possible effects of non-determinism of each argument are combined. See Control Flow and Non-determinism.
Errors: In pure TLA+, the result is undefined if either conjunct evaluates to a non-Boolean value (the evaluation is lazy). In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
TRUE /\ TRUE \* TRUE
FALSE /\ TRUE \* FALSE
TRUE /\ FALSE \* FALSE
FALSE /\ FALSE \* FALSE
FALSE /\ 1 \* FALSE in TLC, type error in Apalache
1 /\ FALSE \* error in TLC, type error in Apalache
Example in Python:
>>> True and True
True
>>> False and True
False
>>> True and False
False
>>> False and False
False
>>> False and 1 # 1 is cast to True
False
>>> 1 and False # 1 is cast to True
False
Special syntax form: To minimize the number of parentheses, conjunction can be written in the indented form:
/\ F_1
/\ G_1
...
/\ G_k
/\ F_2
...
/\ F_n
Similar to scopes in Python, the TLA+ parser groups the expressions according
to the number of spaces in front of /\. The formula in the above example
is equivalent to:
F_1 /\ (G_1 /\ ... /\ G_k) /\ F_2 /\ ... /\ F_n
Or (disjunction)
Notation: F \/ G or F \lor G
LaTeX notation: 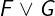
Arguments: Two or more Boolean expressions.
Apalache type: (Bool, Bool) => Bool
Effect:
The binary case F \/ G evaluates to:
-
FALSE, if bothFandGevaluate toFALSE. -
TRUE, ifFevaluates toTRUE, orFevaluates toFALSEandGevaluates toTRUE.
The general case F_1 \/ ... \/ F_n can be understood by evaluating
the expression F_1 \/ (F_2 \/ ... \/ (F_{n-1} \/ F_n)...).
Determinism: deterministic, if the arguments may not update primed variables. If the arguments may update primed variables, disjunctions may result in non-determinism, see Control Flow and Non-determinism.
Errors: In pure TLA+, the result is undefined, if a non-Boolean argument is involved in the evaluation (the evaluation is lazy). In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
TRUE \/ TRUE \* TRUE
FALSE \/ TRUE \* TRUE
TRUE \/ FALSE \* TRUE
FALSE \/ FALSE \* FALSE
TRUE \/ 1 \* TRUE in TLC, type error in Apalache
1 \/ TRUE \* error in TLC, type error in Apalache
Example in Python:
>>> True or True
True
>>> False or True
True
>>> True or False
True
>>> False or False
False
Special syntax form: To minimize the number of parentheses, disjunction can be written in the indented form:
\/ F_1
\/ G_1
...
\/ G_k
\/ F_2
...
\/ F_n
Similar to scopes in Python, the TLA+ parser groups the expressions according
to the number of spaces in front of \/. The formula in the above example
is equivalent to:
F_1 \/ (G_1 \/ ... \/ G_k) \/ F_2 \/ ... \/ F_n
The indented form allows you to combine conjunctions and disjunctions:
\/ /\ F
/\ G
\/ \/ H
\/ J
The above formula is equivalent to:
(F /\ G) \/ (H \/ J)
Negation
Notation: ~F or \neg F or \lnot F
LaTeX notation: 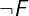
Arguments: One argument that should evaluate to a Boolean value.
Apalache type: Bool => Bool
Effect:
The value of ~F is computed as follows:
- if
Fis evaluated toFALSE, then~Fis evaluated toTRUE, - if
Fis evaluated toTRUE, then~Fis evaluated toFALSE.
Determinism: Deterministic.
Errors: In pure TLA+, the result is undefined, if the argument evaluates to a non-Boolean value. In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
~TRUE \* FALSE
~FALSE \* TRUE
~(1) \* error in TLC, type error in Apalache
Example in Python:
>>> not True
False
>>> not False
True
Implication
Notation: F => G
LaTeX notation: 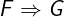
Arguments: Two arguments. Although they can be arbitrary expressions, the result is only defined when both arguments are evaluated to Boolean values.
Apalache type: (Bool, Bool) => Bool.
Note that the => operator at the type level expresses the relation of inputs types to output types for operators,
and as opposed to the => expressing the implication relation at the value level.
Effect: F => G evaluates to:
-
TRUE, ifFevaluates toFALSE, orFevaluates toTRUEandGevaluates toTRUE. -
FALSE, ifFevaluates toTRUEandGevaluates toFALSE.
Determinism: Deterministic.
Errors: In pure TLA+, the result is undefined, if one of the arguments evaluates to a non-Boolean value. In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
FALSE => TRUE \* TRUE
TRUE => TRUE \* TRUE
FALSE => FALSE \* TRUE
TRUE => FALSE \* FALSE
FALSE => 1 \* TRUE in TLC, type error in Apalache
TRUE => 1 \* runtime error in TLC, type error in Apalache
1 => TRUE \* runtime error in TLC, type error in Apalache
Example in Python:
Recall that A => B is equivalent to ~A \/ B.
>>> (not False) or True
True
>>> (not True) or True
True
>>> (not False) or False
True
>>> (not True) or False
False
Equivalence
Notation: F <=> G or F \equiv G
LaTeX notation:  or
or 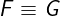
Arguments: Two arguments. Although they can be arbitrary expressions, the result is only defined when both arguments are evaluated to Boolean values.
Apalache type: (Bool, Bool) => Bool
Effect: F <=> G evaluates to:
-
TRUE, if bothFandGevaluate toTRUE, or bothFandGevaluate toFALSE. -
FALSE, if one of the arguments evaluates toTRUE, while the other argument evaluates toFALSE.
How is F <=> G different from F = G? Actually, F <=> G is equality
that is defined only for Boolean values. In other words, if F and G are
evaluated to Boolean values, then F <=> G and F = G are evaluated to the
same Boolean value. We prefer F <=> G to F = G, as F <=> G clearly
indicates the intended types of F and G and thus makes the logical
structure more obvious.
Determinism: Deterministic.
Errors: In pure TLA+, the result is undefined, if one of the arguments evaluates to a non-Boolean value. In this case, Apalache statically reports a type error, whereas TLC reports a runtime error.
Example in TLA+:
FALSE <=> TRUE \* FALSE
TRUE <=> TRUE \* TRUE
FALSE <=> FALSE \* TRUE
TRUE <=> FALSE \* TRUE
FALSE <=> 1 \* runtime error in TLC, type error in Apalache
1 <=> TRUE \* runtime error in TLC, type error in Apalache
Example in Python:
Assume that both expressions are Boolean. Then, in TLA+, F <=> G is
equivalent to F = G. In Python, we express Boolean equality using ==.
>>> False == True
False
>>> True == True
True
>>> False == False
True
>>> True == False
False