Logic

[Back to all operators]

In this section, you find the operators that – together with Sets – form the foundation of TLA+. It is a bit strange that we call this section "Logic", as the whole language of TLA+ is a logic. However, the operators of this section are often seen in first-order logic, as opposed to propositional logic (see Booleans).

Note that the special form \E y \in S: x' = y is often used to express non-determinism in TLA+. See Control Flow and Non-determinism. In this section, we only consider the deterministic use of the existential quantifier.

Bounded universal quantifier

Notation: \A x \in S: P

LaTeX notation: 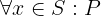forall-bounded

Arguments: At least three arguments: a variable name, a set, and an expression. As usual in TLA+, if the second argument is not a set, the result is undefined. You can also use multiple variables and tuples, see Advanced syntax.

Apalache type: The formal type of this operator is a bit complex. Hence, we give an informal description:

x has the type a, for some type a,
S has the type Set(a),
P has the type Bool,
the expression \A x \in S: P has the type Bool.

Effect: This operator evaluates to a Boolean value. We explain semantics only for a single variable:

\A x \in S: P evaluates to TRUE, if for every element e of S, the expression P evaluates to TRUE against the binding [x |-> e].
Conversely, \A x \in S: P evaluates to FALSE, if there exists an element e of S that makes the expression P evaluate to FALSE against the binding [x |-> e].

Importantly, when S = {}, the expression \A x \in S: P evaluates to TRUE, independently of what is written in P. Likewise, when {x \in S: P} = {}, the expression \A x \in S: P evaluates to TRUE.

Determinism: Deterministic.

Errors: Pure TLA+ does not restrict the operator arguments. TLC flags a model checking error, if S is infinite. Apalache produces a static type error, if the type of elements of S is not compatible with the type of x that is expected in the predicate P.

Advanced syntax: Instead of a single variable x, you can use the tuple syntax to unpack variables from a Cartesian product, see Tuples. For instance, one can write \A <<x, y>> \in S: P. In this case, for every element e of S, the variable x is bound to e[1] and y is bound to e[2]. The predicate P is evaluated against this binding.

Moreover, instead of introducing one variable, one can quantify over several sets. For instance, you can write: \A x \in S, y \in T: P. This form is simply syntax sugar for the form with nested quantifiers: \A x \in S: \A y \in T: P. Similarly, \A x, y \in S: P is syntax sugar for \A x \in S: \A y \in S: P.

Example in TLA+:

  \A x \in {1, 2, 3, 4}:
    x > 0
  \* TRUE
  \A x \in {1, 2, 3, 4}:
    x > 2
  \* FALSE
  \* check the section on tuples to understand the following syntax
  \A <<x, y>> \in { 1, 2 } \X { 3, 4 }:
    x < y
  \* TRUE

Example in Python: Python conveniently offers us a concise syntax:

>>> S = {1, 2, 3, 4}
>>> all(x > 0 for x in S)
True
>>> all(x > 2 for x in S)
False
>>> T2 = {(x, y) for x in [1, 2] for y in [3, 4]}
>>> all(x < y for (x, y) in T2)
True

Bounded existential quantifier

Notation: \E x \in S: P

LaTeX notation: 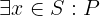exists-bounded

Apalache type: The formal type of this operator is a bit complex. Hence, we give an informal description:

x has the type a, for some type a,
S has the type Set(a),
P has the type Bool,
the expression \E x \in S: P has the type Bool.

Effect: This operator evaluates to a Boolean value. We explain semantics only for a single variable:

\E x \in S: P evaluates to TRUE, if there is an element e of S that makes the expression P evaluate to TRUE against the binding [x |-> e].
Conversely, \E x \in S: P evaluates to FALSE, if for all elements e of S, the expression P evaluate to FALSE against the binding [x |-> e].

Importantly, when S = {}, the expression \E x \ in S: P evaluates to FALSE, independently of what is written in P. Likewise, when {x \in S: P} = {}, the expression \E x \ in S: P evaluates to FALSE.

As you probably have noticed, \E x \in S: P is equivalent to ~(\A x \in S: ~P), and \A x \in S: P is equivalent to ~(\E x \in S: ~P). This is called duality in logic. But take care! If \E x \in S: P may act as a non-deterministic assignment, duality does not work anymore! See Control Flow and Non-determinism.

Determinism: Deterministic when P contains no action operators (including the prime operator '). For the non-deterministic case, see Control Flow and Non-determinism.

Errors: Pure TLA+ does not restrict the operator arguments. TLC flags a model checking error, if S is infinite. Apalache produces a static type error, if the type of elements of S is not compatible in the context of P when an element of S is bound to x.

Advanced syntax: Instead of a single variable x, you can use the tuple syntax to unpack variables from a Cartesian product, see Tuples. For instance, one can write \E <<x, y>> \in S: P. In this case, for every element e of S, the variable x is bound to e[1] and y is bound to e[2]. The predicate P is evaluated against this binding.

Moreover, instead of introducing one variable, one can quantify over several sets. For instance, you can write: \E x \in S, y \in T: P. This form is simply syntax sugar for the form with nested quantifiers: \E x \in S: \E y \in T: P. Similarly, \E x, y \in S: P is syntax sugar for \E x \in S: \E y \in S: P.

Example in TLA+:

  \E x \in {1, 2, 3, 4}:
    x > 0
  \* TRUE
  \E x \in {1, 2, 3, 4}:
    x > 2
  \* TRUE
  \* check the section on tuples to understand the following syntax
  \E <<x, y>> \in { 1, 2 } \X { 3, 4 }:
    x < y
  \* TRUE

Example in Python: Python conveniently offers us a concise syntax:

>>> S = {1, 2, 3, 4}
>>> any(x > 0 for x in S)
True
>>> any(x > 2 for x in S)
True
>>> T2 = {(x, y) for x in [1, 2] for y in [3, 4]}
>>> any(x < y for (x, y) in T2)
True

Equality

A foundational operator in TLA+

Notation: e_1 = e_2

LaTeX notation: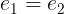

Arguments: Two arguments.

Apalache type: (a, a) => Bool, for some type a.

Effect: This operator evaluates to a Boolean value. It tests the values of e_1 and e_2 for structural equality. The exact effect depends on the values of e_1 and e_2. Let e_1 and e_2 evaluate to the values v_1 and v_2. Then e_1 = e_2 evaluates to:

If v_1 and v_2 are Booleans, then e_1 = e_2 evaluates to v_1 <=> v_2.
If v_1 and v_2 are integers, then e_1 = e_2 evaluates to TRUE if and only if v_1 and v_2 are exactly the same integers.
If v_1 and v_2 are strings, then e_1 = e_2 evaluates to TRUE if and only if v_1 and v_2 are exactly the same strings.
If v_1 and v_2 are sets, then e_1 = e_2 evaluates to TRUE if and only if the following expression evaluates to TRUE:
```
v_1 \subseteq v_2 /\ v_2 \subseteq v_1
```
If v_1 and v_2 are functions, tuples, records, or sequences, then e_1 = e_2 evaluates to TRUE if and only if the following expression evaluates to TRUE:
```
  DOMAIN v_1 = DOMAIN v_2 /\ \A x \in DOMAIN v_1: v_1[x] = v_2[x]
```
In other cases, e_1 = e_2 evaluates to FALSE if the values have comparable types.
TLC and Apalache report an error if the values have incomparable types.

Determinism: Deterministic, unless e_1 has the form x', which can be interpreted as an assignment to the variable x'. For the non-deterministic case, see Control Flow and Non-determinism.

Errors: Pure TLA+ does not restrict the operator arguments. TLC flags a model checking error, if e_1 and e_2 evaluate to incomparable values. Apalache produces a static type error, if the types of e_1 and e_2 do not match.

Example in TLA+:

  FALSE = FALSE         \* TRUE
  FALSE = TRUE          \* FALSE
  10 = 20               \* FALSE
  15 = 15               \* TRUE
  "Hello" = "world"     \* FALSE
  "Hello" = "hello"     \* FALSE
  "Bob" = "Bob"         \* TRUE
  { 1, 2 } = { 2, 3}    \* FALSE
  { 1, 2 } = { 2, 1}    \* TRUE
  { 1 } \ { 1 } = { "a" } \ { "a" } \* TRUE in pure TLA+ and TLC,
                                    \* type error in Apalache
  { { 1, 2 } } = { { 1, 2, 2, 2 } } \* TRUE
  <<1, "a">> = <<1, "a">>           \* TRUE
  <<1, "a">> = <<1, "b">>           \* FALSE
  <<1, FALSE>> = <<2>>              \* FALSE in pure TLA+ and TLC,
                                    \* type error in Apalache
  <<1, 2>> = <<1, 2, 3>>            \* FALSE in pure TLA+ and TLC,
                                    \* FALSE in Apalache, when both values
                                    \* are treated as sequences
  [ a |-> 1, b |-> 3 ] = [ a |-> 1, b |-> 3 ]           \* TRUE
  [ a |-> 1, b |-> 3 ] = [ a |-> 1 ]                    \* FALSE
  [ x \in 2..2 |-> x + x ] = [ x \in {2} |-> 2 * x ]    \* TRUE
  [ x \in 2..3 |-> x + x ] = [ x \in {2, 3} |-> 2 * x ] \* TRUE

Example in Python: The standard data structures also implement structural equality in Python, though we have to be careful to use == instead of =:

>>> False == False
True
>>> False == True
False
>>> 10 == 20
False
>>> 15 == 15
True
>>> "Hello" == "world"
False
>>> "Hello" == "hello"
False
>>> "Bob" == "Bob"
True
>>> { 1, 2 } == { 2, 3 }
False
>>> { 1, 2 } == { 2, 1 }
True
>>> { 1 } - { 1 } == { "a" } - { "a" }
True
>>> { frozenset({ 1, 2 }) } == { frozenset({ 1, 2, 2, 2 }) }
True
>>> (1, "a") == (1, "a")
True
>>> (1, "a") == (1, "b")
False
>>> (1, False) == (2, )
False
>>> (1, 2) == (1, 2, 3)
False
>>> { "a": 1, "b": 3 } == { "a": 1, "b": 3 }
True
>>> { "a": 1, "b": 3 } == { "a": 1 }
False
>>> { x: (x + x) for x in { 2 } } == { x: (x * x) for x in { 2 } }
True
>>> { x: (x + x) for x in { 2, 3 } } == { x: 2 * x for x in { 2, 3 } }
True

Inequality

Notation: e_1 /= e_2 or e_1 # e_2

LaTeX notation: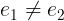

Arguments: Two arguments.

Apalache type: (a, a) => Bool, for some type a.

Effect: This operator is syntax sugar for ~(e_1 = e_2). Full stop.

Bounded Choice

This operator causes a lot of confusion. Read carefully!

Notation: CHOOSE x \in S: P

LaTeX notation: 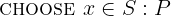choose-bounded

Arguments: Three arguments: a variable name, a set, and an expression.

Apalache type: The formal type of this operator is a bit complex. Hence, we give an informal description:

x has the type a, for some type a,
S has the type Set(a),
P has the type Bool,
the expression CHOOSE x \in S: P has the type a.

Effect: This operator implements a black-box algorithm that somehow picks one element from the set {x \in S: P}. Is it an algorithm? Yes! CHOOSE x \in S: P is deterministic. When you give it two equal sets and two equivalent predicates, CHOOSE produces the same value. Formally, the only known property of CHOOSE is as follows (which is slightly more general than what we wrote above):

  {x \in S: P} = {y \in T: Q} =>
      (CHOOSE x \in S: P) = (CHOOSE y \in T: Q)

Importantly, when {x \in S: P} = {}, the expression CHOOSE x \ in S: P evaluates to an undefined value.

How does CHOOSE actually work? TLA+ does not fix an algorithm for CHOOSE by design. Maybe it returns the first element of the set? Sets are not ordered, so there is no first element.

Why should you use CHOOSE? Actually, you should not. Unless you have no other choice 🎀

There are two common use cases, where the use of CHOOSE is well justified:

Use case 1: Retrieving the only element of a singleton set. If you know that Cardinality({x \in S: P}) = 1, then CHOOSE x \in S: P returns the only element of {x \in S: P}. No magic. For instance, see: Min and Max in FiniteSetsExt.
Use case 2: Enumerating set elements in a fixed but unknown order. For instance, see: ReduceSet in FiniteSetsExt.

In other cases, we believe that CHOOSE is bound to do Program synthesis. So TLC does some form of synthesis by brute force when it has to evaluate CHOOSE.

Determinism: Deterministic. Very much deterministic. Don't try to model non-determinism with CHOOSE. For non-determinism, see: Control Flow and Non-determinism.

Apalache picks a set element that satisfies the predicate P, but it does not guarantee the repeatability property of CHOOSE. It does not guarantee non-determinism either. Interestingly, this behavior does not really make a difference for the use cases 1 and 2. If you believe that this causes a problem in your specification, open an issue...

Example in TLA+:

  CHOOSE x \in 1..3: x >= 3
  \* 3
  CHOOSE x \in 1..3:
    \A y \in 1..3: y >= x
  \* 1, the minimum
  CHOOSE f \in [ 1..10 -> BOOLEAN ]:
    \E x, y \in DOMAIN f:
      f[x] /\ ~f[y]
  \* some Boolean function from 1..10 that covers FALSE and TRUE

Example in Python: Python does not have anything similar to CHOOSE. The closest possible solution is to sort the filtered set by the string values and pick the first one (or the last one). So we have introduced a particular way of implementing CHOOSE, see choose.py:

# A fixed implementation of CHOOSE x \in S: TRUE
# that sorts the set by the string representation and picks the head
def choose(s):
    lst = sorted([(str(e), e) for e in s], key=(lambda pair: pair[0]))
    (_, e) = lst[0]
    return e


if __name__ == "__main__":
    s = { 1, 2, 3}
    print("CHOOSE {} = {}".format(s, choose(s)))
    s2 = { frozenset({1}), frozenset({2}), frozenset({3})}
    print("CHOOSE {} = {}".format(s2, choose(s2)))

Unbounded universal quantifier

Notation: \A x: P

LaTeX notation: 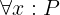forall

Arguments: At least two arguments: a variable name and an expression.

Effect: This operator evaluates to a Boolean value. It evaluates to TRUE, when every element in the logical universe makes the expression P evaluate to TRUE against the binding [x |-> e]. More precisely, we have to consider only the elements that produced a defined result when evaluating P.

Neither TLC, nor Apalache support this operator. It is impossible to give operational semantics for this operator, unless we explicitly introduce the universe. It requires a first-order logic solver. This operator may be useful when writing proofs with TLAPS.

Unbounded existential quantifier

Notation: \E x: P

LaTeX notation: 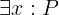exists

Arguments: At least two arguments: a variable name and an expression.

Effect: This operator evaluates to a Boolean value. It evaluates to TRUE, when at least one element in the logical universe makes the expression P evaluate to TRUE against the binding [x |-> e]. More precisely, we have to consider only the elements that produced a defined result when evaluating P.

Unbounded CHOOSE

Notation: CHOOSE x: P

LaTeX notation: CHOOSE x: P

Arguments: At least two arguments: a variable name and an expression.

Effect: This operator evaluates to some value v in the logical universe that evaluates P to TRUE against the binding [x |-> v].

Neither TLC, nor Apalache support this operator. It is impossible to give operational semantics for this operator, unless we explicitly introduce the universe and introduce a fixed rule for enumerating its elements.

Congratulations! You have reached the bottom of this page. If you want to learn more about unbounded CHOOSE, read Section 16.1.2 of Specifying Systems.

Apalache Documentation